ParamCurve - Immersives Lernen von Parameterkurven
Im Projekt „Immersive Learning“ an der Hochschule Kaiserslautern wurden die Materialen des Moduls „Computerorientierte Mathematik“ als Basis verwendet, um eine immersive VR-Lernapplikation mit dem Thema „Parameterkurven“ zu entwickeln.
Eckdaten
Kann Lösungsansätze für folgende Problemstellungen der Lehre bieten:
- Hohe Komplexität der Lerninhalte
- Geringe Lernmotivation
- Passivität der Studierenden
Eignet sich für folgende Virtualisierungsgrade:
- Anreicherung
Nutzt folgende Medieneigenschaften zur Unterstützung des Lernprozesses:
In Universitäten und Hochschulen werden mathematische Konzepte meist unter Verwendung traditioneller Hilfsmittel wie Papier, Tafel und Folien unterrichtet. Zwar werden diese Unterrichtseinheiten oft durch digitale Lernkonzepte unterstützt, jedoch sind diese meist auf passive Visualisierungen wie Videos oder Bilder begrenzt.
Die virtuelle Realität (Virtual Reality, VR) bietet hier neue Möglichkeiten für interaktive Lehransätze. Damit können neue Lerntechniken entwickelt werden, die das räumliche Verständnis fördern und konzeptionelles Denken, welches über rein mathematische Begriffsbildungen hinausgeht, begünstigen.
In diesem vorgestellten Praxisbeispiel wurde das vorhandene Material für eine Lehrveranstaltung im Rahmen des Moduls „Computerorientierte Mathematik“ im Masterstudiengang „Informatik“ an der Hochschule Kaiserslautern als Basis verwendet, um eine immersive VR-Lernapplikation mit dem Thema „Parameterkurven“ zu konzeptionieren und zu entwickeln.
Medieneigenschaften zur Unterstützung des Lernprozesses
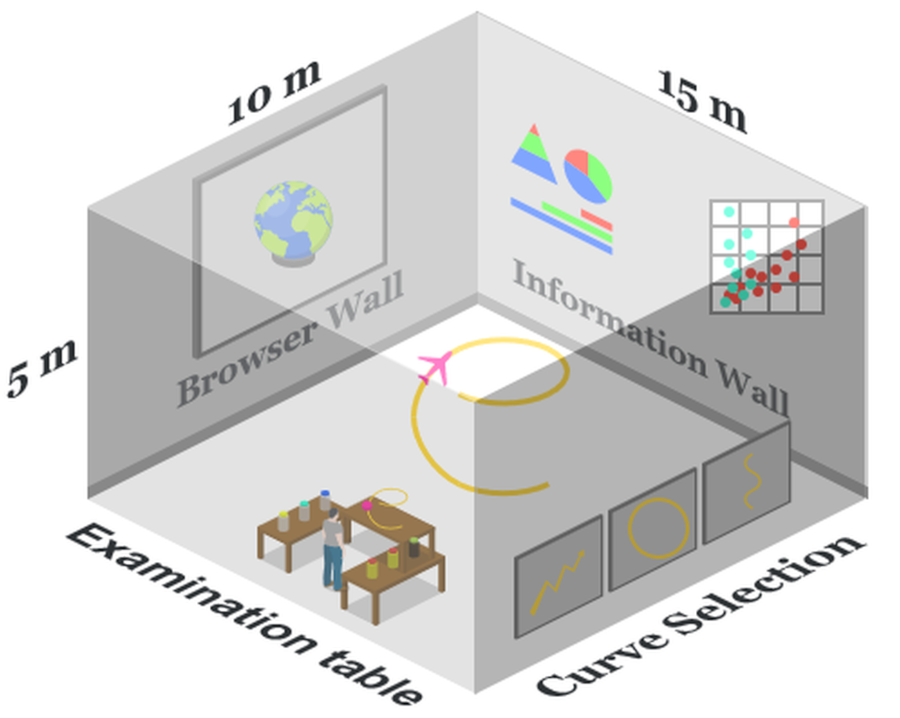
Die VR-Umgebung „ParamCurve“ erlaubt den Studierenden die mathematische Thematik im dreidimensionalen Raum zu erleben und mit den mathematischen Konstrukten zu interagieren. Parameterkurven werden im Raum dargestellt und können manipuliert und befahren werden.
Die aktuelle Version erhebt keine Nutzungsdaten zur Anpassung der Lernumgebung an die Lernenden. Jedoch existieren bereits interaktive Aufgabenmodelle, die zukünftig an die Lernenden angepasst werden können.
Die Anwendung erlaubt Aufgabenmodelle, in denen Anwender/innen mit Lernenden außerhalb der virtuellen Realität synchron kommunizieren, um gemeinsam gestellte Aufgaben lösen zu können.
Derzeit wird der Inhalt einer Lerneinheit fest vorgegeben. In Zukunft besteht auch die Möglichkeit, den gesamten Stamm an Lerninhalten für die Studierenden freizugeben, um eine selbstmotivierte und selbstgesteuerte Aneignung des Lehrstoffs zu erlauben.
Lösungsansätze für Problemstellungen der Lehre
Für die folgenden Problemstellungen kann das Praxisbeispiel Lösungsansätze bieten:
- Hohe Komplexität der Lerninhalte:
Mathematische Konzepte werden von einem Teil der Lernenden stets als komplex und schwierig eingestuft. Interaktive Anwendungen in VR eignen sich gut, um geometrische Konstrukte darzustellen und generelles Wissen über die mathematische Formel hinaus zu fördern.
- Geringe Lernmotivation:
Die virtuelle Realität weckt aktuell bei Studierenden ein inhärentes Interesse, Inhalte in diesem Medium zu erleben. Ebenfalls profitieren Studierende oft von jeglicher Art der Visualisierung und alternativer Darstellung von mathematischen Konzepten.
- Passivität der Studierenden:
Virtuelle Umgebungen erlauben den Studierenden, mit dem Lehrstoff auf eine andere Art wie in traditionellen Lernszenarien zu interagieren. Eine aktive Teilnahme wird gefördert, da Studierenden sich aktiv mit Händen, Kopf und Körper in der virtuellen Lernumgebung bewegen und mit ihr interagieren.
Virtualisierungsgrad
Der Virtualisierungsgrad beschreibt das Verhältnis von analogen und digitalen Elementen in einem Lehr-/Lernszenario. Das Praxisbeispiel unterstützt die folgenden Virtualisierungsgrade:
- Anreicherung
Ressourcen
Soft- und Hardware
- Python 3, Unity Engine, VR-Brillen (HTC VIVE Focus Plus)
Weitere Informationen zum Praxisbeispiel
Kontakt
Sie möchten mehr über das Praxisbeispiel erfahren? Hier können Sie Kontakt zu den Autorinnen und Autoren aufnehmen:
Prof. Manfred Brill
Hochschule Kaiserslautern
Informatik
Amerikastraße 1
66482 Zweibrücken
Mail: manfred.brill@hs-kl.de
Benedict Särota, M. Sc.
Hochschule Kaiserslautern
Informatik
Amerikastraße 1
66482 Zweibrücken
Mail: benedict.saerota@hs-kl.de